Email chain of correspondence with Stan and Philip
Original email subject
We want to give you a heads up about a paper we are writing. :::::: Toward Accurate Dynamic Time Warping in Linear Time and Space
Go back to the supporting page for FastDTW is approximate and Generally Slower than the Algorithm it Approximates.
Eamonn on Feb. 13, 2020, 12:58
Hi Philip
I have been playing around with FastDTW.
One issue I have is that it is slow because of the overhead of recursion.
Do you have an non-recursive version? (of have you every seen one somewhere?)
Many thanks, eamonn
Philip on Feb. 14, 2020, 14:08
Thanks for your interests. Our versions are posted at:
code.google.com/archive/p/fastdtw/downloads
A quick search indicates other versions, which I don’t know are recursive or not.
Stan on Feb. 18, 2020, 11:18
Eamonn,
I doubt that this removes the recursion, but this project is likely to have a much faster implementation than my **old** java version: https://github.com/slaypni/fastdtw
I haven’t contributed to the project myself and am not completely familiar with it, but I think it is a pretty efficient python fastdtw package that is actually wrapping C++ for efficiency. I’ve seen some bug reports where if there are some issues (that I don’t understand) the c++ compilation won’t work and it falls back onto a full-python implementation on install which will make it run slower (but will still get the same results)
hopefully this helps,
Stan
Eamonn on Feb. 21, 2020, 18:10
Dear Philip and Stan.
We want to give you a heads up about a paper we are writing.
We think that FastDTW is actually slower than simple DTW, implemented with an iterative version (not recursion).
Moreover, the differences are not small, simple DTW is a lot faster.
(to be clear, I am not talking about the amortized cost for sliding window search, where DTW would be thousands of times faster. I just mean the comparison of any two time series )
We therefore think the community should use the faster and exact method, and our paper advocates that.
We want to be scrupulously fair to you and your paper.
If we have made an error, please let us now, and we will fix it.
If you want us to run a different version of your code, or use special data, or use special settings, please tell us, and we will do so.
It is a little bit unusual to write a paper to explicitly suggest that the community abandon an idea. However, this idea may now be holding back research (see examples in paper).
If you are on board with our message, and want to contribute, perhaps you could join us as coauthors…
eamonn
Stan on Feb. 25, 2020, 19:34
Eamonn,
I have some thoughts:
- I don’t think the “recursive” vs. “iterative” aspect is relevant to things being slow. The number of recursive calls for a billion-length time series would only be 23 which is not really a lot of recursion … it’s a ~3 disc Tower of Hanoi or “fibonacci(6)=8” amount of recursion.
- “the constant factor is quite large” (for r=10, interpreting it as a radius so the total window size is 2*r+1)
- FastDTW: 8*r+10=90, (10 instead of 14 to ignore the time required to trace the warp path that is identical to cDTW)
- cDTW: 2*r+1=21
- ^the constant factor is not 94X higher than cDTW… it’s more like 4.3X higher (based on the number of cost matrix cells filled-in) which I feel is a pretty reasonable constant factor for something that can find a flexible path through any part of the cost matrix similar to the full DTW algorithm. FastDTW also evaluates a “window” at the full resolution that is twice the width of a comparable parameter r for cDTW… so the true constant factor is ~2.1X that of cDTW with the same size amount of constraint in the cost matrix.
- “The iterative version only requires O(n) space” - FastDTW and cDTW both have the same space complexity: O(N). FastDTW is more specifically ~2X the complexity of cDTW for the same value of “r” due to the way that it interprets the parameter.
- the FastDTW java implementation is pretty old, this is the implementation more people would be using these days: https://github.com/slaypni/fastdtw (I haven’t contributed to or used this repo myself).
- Some results on their implementation that indicates FastDTW is faster than fullDTW for lengths greater than around 300 which is about what we originally reported in the paper: https://github.com/slaypni/fastdtw/issues/38 If there are some c++ compilation issues for the cython python library during install it’s possible it will fall back to an all-python implementation which would be very slow, but hopefully the install will “just work”
- I’m all for warning people away from using the research paper implementation of FastDTW in favor of the link above or translations by others (but it’s OK for a reference). It’s written in a very old version of Java that is not memory efficient and all tests were run in the 32-bit dark ages when single process couldn’t access much memory even if the machine had it and java had some memory limitations on top of that (which is why the weird on-disk swap thing was necessary for long time series).
- FastDTW radius and cDTW radius are not directly comparable for the same radius value. At any radius, FastDTW can find a warp path that traverses any path in the full cost matrix… while in cDTW it is constrained to go down the diagonal of the cost matrix and any fixed size radius for cDTW begins to consider only a vanishingly small percentage of the cost matrix as the length of the time series increases to large sizes and converges towards just being a euclidean distance measurement.
- I agree that more useful results are often obtained by using constrained DTW (depending on the use case), and simply sampling the time series is often acceptable. But if the time series cannot be downsampled and the warp path is not guaranteed to be very close to a linear warp, then FastDTW is required in the case of very long time series. These two conditions made FastDTW necessary for a subset of data we were using for one of our projects, had some important short sequences that we thought needed to be aligned at full resolution without sampling, and the warp path could be far from a linear warp path. I can’t say how often this criteria is met where FastDTW is necessary/better than DTW, but it was necessary for our use case and I am sure that there are others out there.
- “However, this measure has a serious logic bug, in that it allows both arbitrarily bad false positives and false negatives” - the measure is determining how similar FastDTW’s results match the standard DTW algorithm, not how well the (Fast)DTW cost works for classification on a particular test set.
- “What should that metric be? The answer is usually the difference between the distance returns by DTW and FastDTW” - I don’t see how this is different than what was argued against in the previous bullet
Stan
Eamonn on Feb. 25, 2020, 21:33
- I don’t think the “recursive” vs. “iterative” aspect is relevant to things being slow. The number of recursive calls for a billion-length time series would only be 23 which is not really a lot of recursion … it’s a ~3 disc Tower of Hanoi or “fibonacci(6)=8” amount of recursion.
Yes, you are correct. We implemented FastDTW with an iterative implementation. It takes a lot less memory, but is just as slow. However, we assume you compared to “classic” DTW with an interactive implantation, which explains why you found DTW to be slow.
- “the constant factor is quite large” (for r=10, interpreting it as a radius so the total window size is 2*r+1)
- FastDTW: 8*r+10=90, (10 instead of 14 to ignore the time required to trace the warp path that is identical to cDTW)
- cDTW: 2*r+1=21
- ^the constant factor is not 94X higher than cDTW… it’s more like 4.3X higher (based on the number of cost matrix cells filled-in) which I feel is a pretty reasonable constant factor for something that can find a flexible path through any part of the cost matrix similar to the full DTW algorithm. FastDTW also evaluates a “window” at the full resolution that is twice the width of a comparable parameter r for cDTW… so the true constant factor is ~2.1X that of cDTW with the same size amount of constraint in the cost matrix.
- “The iterative version only requires O(n) space” - FastDTW and cDTW both have the same space complexity: O(N). FastDTW is more specifically ~2X the complexity of cDTW for the same value of “r” due to the way that it interprets the parameter.
If that is so, why does it give a memory error for long time series, but cDTW does not,even for time series that are ten time longer?
- the FastDTW java implementation is pretty old, this is the implementation more people would be using these days: https://github.com/slaypni/fastdtw (I haven’t contributed to or used this repo myself).
- Some results on their implementation that indicates FastDTW is faster than fullDTW for lengths greater than around 300 which is about what we originally reported in the paper: https://github.com/slaypni/fastdtw/issues/38 If there are some c++ compilation issues for the cython python library during install it’s possible it will fall back to an all-python implementation which would be very slow, but hopefully the install will “just work”
Renjie, can you try to grab this code and run it?
- I’m all for warning people away from using the research paper implementation of FastDTW in favor of the link above or translations by others (but it’s OK for a reference). It’s written in a very old version of Java that is not memory efficient and all tests were run in the 32-bit dark ages when single process couldn’t access much memory even if the machine had it and java had some memory limitations on top of that (which is why the weird on-disk swap thing was necessary for long time series).
- FastDTW radius and cDTW radius are not directly comparable for the same radius value. At any radius, FastDTW can find a warp path that traverses any path in the full cost matrix… while in cDTW it is constrained to go down the diagonal of the cost matrix and any fixed size radius for cDTW begins to consider only a vanishingly small percentage of the cost matrix as the length of the time series increases to large sizes and converges towards just being a euclidean distance measurement.
This is true, but…
1) When do you need to go so far off the diagonal? We know the best constraints for 128 different public data sets, (https://www.cs.ucr.edu/~eamonn/time_series_data_2018/) and 3/4 of them are less than 5%, 90% are less than 10%.
2) Even if we allow cDTW to explore more of the matrix, it is still faster and exact.
- I agree that more useful results are often obtained by using constrained DTW (depending on the use case), and simply sampling the time series is often acceptable. But if the time series cannot be downsampled and the warp path is not guaranteed to be very close to a linear warp, then FastDTW is required in the case of very long time series. These two conditions made FastDTW necessary for a subset of data we were using for one of our projects, had some important short sequences that we thought needed to be aligned at full resolution without sampling, and the warp path could be far from a linear warp path. I can’t say how often this criteria is met where FastDTW is necessary/better than DTW, but it was necessary for our use case and I am sure that there are others out there.
Can you point to a dataset and experiment that can demonstate this? The only long time series we have ever had to align is music. But in music, you cannot get too far from the diagonal (a few seconds per minute for classical music).
Again, to be clear. If you provide the dataset, we will run and report the experiment.
My lab has published 128 data sets here [a] and about 100 other datasets in other papers, and we have played with a few hundred other datasets. Of course, absence of evidence is not evidence of absence. But it is surprising that we have never found such a dataset.
- “However, this measure has a serious logic bug, in that it allows both arbitrarily bad false positives and false negatives” - the measure is determining how similar FastDTW’s results match the standard DTW algorithm, not how well the (Fast)DTW cost works for classification on a particular test set.
Yes, we know, sorry if that was not clear. However, you cannot use the fidelity to the warping path as a measure, because you can change one time series by an arbitrarily small epsilon, and get a very different warping path.
Or put it another way. Two correct implementations of standard DTW can give identical distances but very different warping paths, depending only on tie breaking policy.
- “What should that metric be? The answer is usually the difference between the distance returns by DTW and FastDTW” - I don’t see how this is different than what was argued against in the previous bullet
Yes, the metric should be how well FastDTW approximates DTW, but your metric does not measure that. As noted, it can produce “ both arbitrarily bad false positives and false negatives “.
The DTW distance is used in 1,000s of algorithms. If you can approximate that distacne fast, you really have something.
Almost no one cares about the warping path (for classification, for clustering etc), so no one cares if you can approximate it (to my knowledge).
And again, it is not clear what it even means to approximate it. Imagine warping ten sine waves to eleven sine waves. There are ten different, but equally good warping paths.
Thanks for your response. We dont want to burden you with emails, but if you want we will send you an updated paper in a few weeks.
eamonn
[a] https://www.cs.ucr.edu/~eamonn/time_series_data_2018/
Philip on Feb. 26, 2020, 09:52
Additional thoughts:
-
Since “radius” might not be compatible among algorithms, we studied % of evaluated cells which is comparable across algorithms and its tradeoff against accuracy/error (with respect to distance obtained from the “original” DTW). This tells us how “well” the algorithms utilize computation.
-
The Gun dataset we used is from your UCR group.
-
If the optimal wrap path is known **before hand** to be near the diagonal, cDTW (constraint DTW with a fixed radius) would be great (linear time and space). What if we don’t know before hand?
Eamonn on Feb. 26, 2020, 10:16
Additional thoughts:
1. Since “radius” might not be compatible among algorithms, we studied % of evaluated cells which is comparable across algorithms and its tradeoff against accuracy/error (with respect to distance obtained from the “original” DTW). This tells us how “well” the algorithms utilize computation.
I think it is “somewhat” comparable. But the overhead to “touch” a cell can variety a lot depending on the algorithm.
and its tradeoff against accuracy/error (with respect to distance obtained from the “original” DTW). This tells us how “well” the algorithms utilize computation.
True in general, but as we noted. Measuring accuracy/error with respect to the warping path is a bad idea.
Look at the accumulative matrix below. There are eight different warp paths, all of which are equally good.
2. The Gun dataset we used is from your UCR group.
yes, it has become the official logo of the lab, see photo below.
3. If the optimal wrap path is known **before hand** to be near the diagonal, cDTW (constraint DTW with a fixed radius) would be great (linear time and space). What if we don’t know before hand?
If we wanted to do full DTW, it would still be faster to use classic DTW than to use FastDTW with a radius of 3. See plot 1 in the paper.

eamonn
Stan on Feb. 26, 2020, 14:38
Eamonn,
comments(v2):
the overhead to “touch” a cell can variety a lot depending on the algorithm
The overhead for FastDTW will be a bit higher for the same number of cell comparisons because it’s not just filling in a single matrix, but FastDTW should be faster than DTW (aligning one thing to another thing, full cost matrix) for lengths larger than 300-1000 (empirically)
Re: running out of memory
I remember now the memory issues related to Java. By default it only allows 64M to be used by a java program (I think this is still currently true), and to let more memory be used “-Xms2g -Xmx2g” parameters must be given when java is run. I think that there is still a 2GB limit on java program even all these years later so in the test I ran here on a 275,000 length time series with a radius of 1000 it wasn’t quite enough to fit in memory.
I dusted off the cobwebs of the old implementation and tried running a 275,000 length time series with a radius of 1000 (to push the memory limits) and got the following results:
FastDTW, radius=1000
- ran: java -Xms2g -Xmx2g com/FastDtwTest trace0.csv-100 trace1.csv-1000 1000
- this radius is much larger than necessary, so it would typically run faster with the ~same results using a smaller radius)
- finished in 2m52.031s
- I got the warning about things not fitting into memory and so it ran using a swap disk (successfully), while running it gave the message: “Ran out of memory initializing window matrix, all cells in the window cannot fit into main memory. Will use a swap file instead (will run ~50% slower)”
cDTW, radius=1000 (window size 2001)
- ran: java -Xms2g -Xmx2g com/BandTest trace0.csv-100 trace1.csv-1000 1000
- finished in 2m8.704s
- I also get an out of memory warning here and it uses the swap disk
- This implementation probably not as optimized as it could be for the specific case of a fixed width window because it is a general implementation that can work with any shape/size window and is saving a min/max j index for each i
“There are eight different warp paths, all of which are equally good”
If they have the same warp cost then DTW (and FastDTW) consider them all to be equally good. There is a good case to be made that they are not equally good in many/most situations, but that is an argument against DTW (not FastDTW).
If we wanted to do full DTW, it would still be faster to use classic DTW than to use FastDTW with a radius of 3. See plot 1 in the paper
I’m not sure exactly what ~”classify all … with iterative cDTW” means exactly. I assume “iterative cDTW with a 100% warp window size” is the same as regular full DTW. There are many techniques to speed up DTW-related similarity search and classification as you know (and largely invented yourself). FastDTW is just speeding up the calculation of one alignment of a long time series and producing a warp path if needed. I assume most of those speedup tricks could also be applied to FastDTW for those use cases… but it’a already fast enough with standard DTW it’d be an unusual use case that would call for it.
we assume you compared to “classic” DTW with an interactive implantation, which explains why you found DTW to be slow
Our Full-dtw implementation was implemented in the standard way (cost matrix is a matrix)
Our windowed/constrained DTW was implemented by keeping track of the min/max indexes for each row in the cost matrix (so we could specify any size/shape path through the cost matrix to evaluate).
Is there a much better way to do it or another approach (align one time series to another using an optional subset through the cost matrix) that I’m not aware of?
3/4 of them [window sizes] are less than 5%, 90% are less than 10%.
For a O(N^2) algorithm, a 10% warp window provides a 90% speedup. A Fixed % speedup for a time complexity that is growing at N^2 is only going to help for so long and doesn’t scale well to large sizes. And as I said earlier a fixed width warp window will converge to a euclidean distance measurement as time series lengths increase.
I’m not arguing for universal usage for FastDTW, for lengths roughly under 200-1000 (depending on the radius) it is slower than DTW, at lengths modestly larger than that it is not much faster and does not guarantee exact results, but for very long time series and in particular where the alignment is as or more important than the alignment cost FastDTW is needed.
It is true that DTW and unconstrained (or loosely constrained) warping is not the best way to approach many/most problems practical, but these issues are in common between DTW and FastDTW. FastDTW only allowing “unconstrained” warping is not necessarily a disadvantage because it would be easy to modify it to also only consider a particular warp window.
Can you point to a dataset and experiment that can demonstate this?
I haven’t worked with time series in a while, but I’ll look at some of the FastDTW citations to see if there are any obvious good examples in there. Having recently (an quickly) run out of space on a 10TB hard drive because of too much data, it’s hard for me to imagine that there are not many use cases (even if they are in the minority) where someone needs to align some numerical sequences together of lengths >1000-10000+.
Speech waveforms may be one possibility … I work on ASR and we definitely do not commonly use DTW for speech recognition anymore other than a few “researchy” use cases like “what if we have *no* training data at all for a rare indonesian language” and we want to be able to recognize N words. A large warp window can be needed if comparing 2 time series that start/stop at varying times, but as long as ONE of the time series is well trimmed a psi parameter can be used to ignore as much or as little from the ends of the other sequence as necessary (I’ve had to use that for some alignment problems… but not numerical time series in my case).
However, you cannot use the fidelity to the warping path as a measure
In the FastDTW paper we only measure the similarity/approximation between DTW and FastDTW by the warping distance because the warp path with the same “quality” warp can vary greatly (as you said)
Almost no one cares about the warping path
This is true in your experience (a lot of classification and similarity search), but I’ve usually cared a bit more about the path than the score in the jobs that I’ve worked on (although my experience has diverged from time series data and more into non-sample-able sequences):
- Aligning sections of several time series to create a “merged” version for display and to cluster related sections of different time series. This was some of the data from our old NASA project where some time series were 20,000 points (took some time for full DTW back then) and could have a lot of variation in the warping path because of variation between the timings of “on” and “off”.
- aligning truth transcripts to hypothesis transcripts to find particular errors and “score” ASR systems (occasionally very long)
- aligning hypothesis phone sequences to one or more expected sequences to detect mispronunciations in language learning
- aligning ASR transcripts (with timestamps from the audio file) to book transcripts or scripts to assign times to each word (for things like Amazon’s whispersync or TV subtitles) ^ although most of these are not numerical time series, so subsampling is not an option and not FastDTW is no an option for those… but it does give some examples of where the warp path is more important (or equally important) than the warp cost.
We dont want to burden you with emails, but if you want we will send you an updated paper in a few weeks.
sure, I’ll also try not to burden you with responses :)
Stan on Feb. 26, 2020, 14:41
fyi, my java version is this, and I used the old code without modification: https://storage.googleapis.com/google-code-archive-downloads/v2/code.google.com/fastdtw/FastDTW-1.1.0.zip
java version "1.7.0_79"
Java(TM) SE Runtime Environment (build 1.7.0_79-b15)
Java HotSpot(TM) 64-Bit Server VM (build 24.79-b02, mixed mode)
^it’s just the version that was already installed on my mac, I haven’t intentionally installed/used Java or the SDK on this computer
Eamonn on Feb. 26, 2020, 15:05
The overhead for FastDTW will be a bit higher for the same number of cell comparisons because it’s not just filling in a single matrix, but FastDTW should be faster than DTW (aligning one thing to another thing, full cost matrix) for lengths larger than 300-1000 (empirically)
We have not observed that. The plot we showed you was Mallat, those time series have a length of 1024. For N= 1024, full matrix computation, DTW is stll faster than FastDTW with radius 3
You say “FastDTW should be faster than DTW”, however, it simply is not the case. We are happy to share our code so you can run it and see.
I think in you mind you are recalling a recursive version of DTW. Yes, that would be slow as molasses! But almost no one has used a recursive version of DTW in decades.
I remember now the memory issues related to Java. By default it only allows 64M to be used by a java program (I think this is still currently true), and to let more memory be used “-Xms2g -Xmx2g” parameters must be given when java is run. I think that there is still a 2GB limit on java program even all these years later so in the test I ran here on a 275,000 length time series with a radius of 1000 it wasn’t quite enough to fit in memory.
Our implement does not run out of memory at an order of magnitude longer queries. The memory overhead of iterative DTW is O(N) with tiny constants.
If they have the same warp cost then DTW (and FastDTW) consider them all to be equally good. There is a good case to be made that they are *not* equally good in many/most situations, but that is an argument against DTW (not FastDTW).
I think I made a mistake here. Your eq [14] is labelled “Error of a warp path”, but it does not look at the warp path. I will correct, thanks.
I’m not sure exactly what ~”classify all … with iterative cDTW” means exactly. I assume “iterative cDTW with a 100% warp window size” is the same as regular full DTW. There are many techniques to speed up DTW-related similarity search
This claim is for ZERO tricks, Just using vanilla cDTW as people were using 20 years ago. The only trick is NOT using recursion, just using the iterative version.
and classification as you know (and largely invented yourself). FastDTW is just speeding up the calculation of one alignment of a long time series and producing a warp path if needed. I assume most of those speedup tricks could also be applied to FastDTW for those use cases
You cannot use the early abandoning trick with recursion.
For a O(N^2) algorithm, a 10% warp window provides a 90% speedup. A Fixed % speedup for a time complexity that is growing at N^2 is only going to help for so long and doesn’t scale well to large sizes. And as I said earlier a fixed width warp window will converge to a euclidean distance measurement as time series lengths increase.
Again, to be clear. With no warp window, DTW is still faster than FastDTW.
I haven’t worked with time series in a while, but I’ll look at some of the FastDTW citations to see if there are any obvious good examples in there.
We have already done this, but a second pair of eyes would always be helpful. We have also looked any more general papers in SIGKDD, ICDM, ICML, SIGMOD, VLDB etc
In the FastDTW paper we only measure the similarity/approximation between DTW and FastDTW by the warping distance because the warp path with the same “quality” warp can vary greatly (as you said)
Again, I made a mistake here, because you titled it “Error of a warp path “ , but I now realize you do not look at the warp path. I will correct, thanks.
eamonn
Stan on Feb. 26, 2020, 16:01
I think in you mind you are recalling a recursive version of DTW. Yes, that would be slow as molasses! But almost no one has used a recursive version of DTW in decades.
It’s a dynamic programming implementation, not recursive (the only implementation I was aware of). I thought previously when you said recursive that you were pointing to the log(n) number of DTW() calls in FastDTW at lower resolutions. If what I’m saying still doesn’t make sense to you I think that means you need to send me a link to a paper for “iterative DTW” 🙂
Stan
Eamonn on Feb. 26, 2020, 16:25
Hmm.
Then, I am confused about how you reported such incredibly slow numbers for DTW.
In your figure 10, you report about 1 second for unconstrained DTW, of length 1,000.
On a modern (but not high end) machine, that takes about 3 milliseconds.
Even in 2007, this should have been well under 0.1 seconds.
If you have that original DTW implementation, we will be happy to test it.
Nevertheless: Here is where we stand:
- We compare FastDTW vs vanilla DTW on a variety of data sets, different lengths, different constraints (and no constraints) etc.
- We find Vanilla DTW is always faster than FastDTW.
- We cannot create a figure like fig 10 of your paper, that shows DTW being slower than FastDTW. This means that..
- Our version of DTW is magically fast. But this surely is not the case, it is pure Vanilla DTW.
- Our version of FastDTW is crippled slow. But this does not seem to be the case. We tried your version, we tried another versions, we tried our own implementation of FastDTW
- Somehow, your version of DTW just happened to be very very slow for some reason.
I think ‘3’ is the most likely explanation.
eamonn
Philip on Feb. 26, 2020, 17:29
We did not measure the error in wrapping paths, we measured the error in distance with respect to the “correct” distance from fullDTW. That is:
algX_distance(T1, T2) vs. fullDTW_distance(T1, T2)
It’s interesting that an O(N) algorithm is slower than an O(N^2) algorithm.
Eamonn on Feb. 26, 2020, 17:45
We did not measure the error in wrapping paths, we measured the error in distance with respect to the “correct” distance from fullDTW. That is:
algX_distance(T1, T2) vs. fullDTW_distance(T1, T2)
Yes, as I mentioned twice in my last email, I misread eq 14, and I have now corrected it.
It’s interesting that an O(N) algorithm is slower than an O(N^2) algorithm.
Yes it is. We are trying to understand this. We are profiling the code.
However, at the end of the day, big oh only speaks about asymptotic performance.
- If you have any ideas to explain the results, we would love to hear them.
- If you want to test on your machine, we will send you all the code
- If you have a faster version of FastDTW, we would love to included it in our experiments.
However. There are some precedents.
For example: Haar wavelets can be computed in O(N) time, but DTW takes O(Nlog(N)) time. However, under almost all circumstances, computing DTW is much faster (partly because most hardware supports it).
eamonn
Stan on Feb. 26, 2020, 23:37
Eamonn,
I found a couple examples skimming the first 2 pages of google results for “FastDTW salvador long time series”:
http://davidanastasiu.net/pdf/papers/2019-Kapoor-asp-tr.pdf
- “Some stimuli have much more than 100,000 data”
- “IDDTW like PDTW is not acceptable for precise alignment of the time series”
- ^time series used not that long though?, but an indications that for some use cases sampling is not acceptable
https://pure.tue.nl/ws/portalfiles/portal/47009585/789179-1.pdf
- “604,800 measurements in one week”??? (not sure what they mean be this exactly)
- they ran DTW on at least length 15,000-100,000 time series
- ^they ran out of memory like you did with FastDTW and had to be a bit create to align the larger time series … java doesn’t like to use RAM (especially without a -Xmx paramater)). A non-Java implementation should have been able to run without memory issues. Reading their comments they may have even been accidentally using the DTW implementation in FastDTW instead of “FastDTW”… but either way they had long time series that they wanted to align.
Testing the Java implementation just now, times include startup and reading text files… In this test it’s worth noting that if I provide a SINGLE element time series it takes 0.113 seconds to run… so it’s about 0.11 seconds just to start up java so things start running. In the paper’s results I used in-program timers that ignore JVM startup time which is why there are are some time measurements <0.05 seconds on that slower computer (today I just used the “time” command)
## Length=1000 ## (java) DTW(full) 0m0.224s
DTW(r=10) 0m0.186s
DTW(r=1000) 0m0.268s
FastDTW(r=10) 0m0.220s
FastDTW(r=1000) 0m0.228s
^all about the same, they can vary between runs, about 2X the time that it takes to run “nothing” in java
## Length=10,000 ## (java)
DTW(full) 0m8.397s <-regular DTW
DTW(r=10) 0m0.365s
DTW(r=10,000) 0m10.567s <-DTW with a window that evaluates everything (there’s some overhead)
FastDTW(r=10) 0m0.495s <-FastDTW is much faster, some modest overhead compared to DTW with the same size window
FastDTW(r=10,000) 0m8.446s <-large window making it evaluate everything… but going through the FastDTW code
^ fastDTW is faster than full DTW with a reasonable radius, a little slower than DTW when evaluating the same number of cells in the cost matrix («2X overhead)
The java version really does seem dumb and limited with memory use
Results below are for this python (not mine) implementation just now for the first time as a sanity check: https://github.com/slaypni/fastdtw
It’s overall slower than I expect, but code being 36X slower in all-python code is (sadly) not too unusual (depending on how much of the code being run is python vs c++) … but the DTW/FastDTW time comparison is generally as expected.
length 10,000 full DTW: 1129.5 sec
length 10,000 FastDTW(radius=10) = 17.9 sec
length 100,000 FastDTW(radius=10) = 178.7 sec
length 1,000,000 FastDTW(radius=10) = 1807.1 sec
^memory use for 1M long time series is around 3.1G (or it may be 380MB actually used… I’m not entirely clear about how memory compression on non-frequently accessed RAM works and should be interpreted in OSX)
We find Vanilla DTW is always faster than FastDTW.
I’m not sure why, but I don’t think that should be the case.
results above are using:
- https://github.com/slaypni/fastdtw (a python version written by others)
- https://storage.googleapis.com/google-code-archive-downloads/v2/code.google.com/fastdtw/FastDTW-1.1.0.zip (the paper Java version with some minor bugfixes)
Stan
Eamonn on Feb. 27, 2020, 00:43
I found a couple examples skimming the first 2 pages of google results for “FastDTW salvador long time series”:
http://davidanastasiu.net/pdf/papers/2019-Kapoor-asp-tr.pdf
- “Some stimuli have much more than 100,000 data”
I am aware of this work. They have NO idea what they are doing. They should not be doing DTW on 100,000 time series, which is why DTW gives them the default rate. They say…
” Even though DTW is an important metric for comparing time series, we observed that classification models based on DTW failed to outperform other classification models in our problem. The best accuracy achieved by the DTW-KNN models was 77.50%, which is approximately 18% lower than that of the best performing model. “
For what it’s worth, we can do 100,000 easily without running out of memory.
Look at the data they show. You cannot meaningfully warp 412 heartbeats to 517 heartbeats, which is basically what they are doing.
- “IDDTW like PDTW is not acceptable for precise alignment of the time series”
- ^time series used not that long though?, but an indications that for some use cases sampling is not acceptable
Not sure what you are pointing to here. I see short alignments of length 120, 500, and 2,000, Which DTW can do, exactly, blindingly fast.
https://pure.tue.nl/ws/portalfiles/portal/47009585/789179-1.pdf
- “604,800 measurements in one week”??? (not sure what they mean be this exactly)
- they ran DTW on at least length 15,000-100,000 time series
- ^they ran out of memory like you did with FastDTW and had to be a bit create to align the larger time series … java doesn’t like to use RAM (especially without a -Xmx paramater)). A non-Java implementation should have been able to run without memory issues. Reading their comments they may have even been accidentally using the DTW implementation in FastDTW instead of “FastDTW”… but either way they had long time series that they wanted to align.
Again, these guys have no idea what they are doing. Many of
However, even they are not suggesting comparing 604,800 measurements in one week, to 604,800 measurements in another week.
” but either way they had long time series that they wanted to align. “ I only see comparisons with length 2,000.
” A bigger problem arose when the algorithm was applied on two time series of 15,000 values: R ran out of memory. “ If they had used vanilla DTW, they would never have written the sentence “(we) ran out of memory “. This is one reason we want to encourage people not to use FastDTW. That way they can explore larger and longer datasets.
The quotes in this paper seem to support our case.
But in any case. We can run DTW on length 15,000, and it is faster and exact.
Sorry, but I stand by my claim. There are no example of long time series, that are meaningfully aligned in an unconstrained warping.
1) There are long time series aligned in music, but the constraint here is always a few seconds, ie 1 or 2 percent.
2) Even for short time series, it is very hard (but not impossible) to find examples that need unconstrained warping.
---
I will take a look at the results below later. But to be clear, what FastDTW code would you like use to use?
Also, do you want to use OUR DTW code? (which is nothing fancy)
cheers
eamonn
Stan on Feb. 27, 2020, 01:24
I will take a look at the results below later. But to be clear, what FastDTW code would you like use to use?
You should probably use the Java version. I did a little bit of googling and figured out the missing argument needed to let Java actually run in 64 bit mode (it runs in 32-bit without setting a special flag).
Running this: “time java -Xmx6g -Xmx6g -d64 com/FastDtwTest x.csv y.csv 10” on a 275,000 length time series finishes in 25 seconds and uses about 290MB of RAM (the result includes the warp path) without having to resort to the sketchy on-disk workaround.
I looked at the code a little for the python version and I think their “DTW” implementation is correct but rather slow. This slows down both DTW and FastDTW by about the same ratio because most of the “work” in FastDTW is done in a call to a regular DTW function that allows custom search windows though the cost matrix to be specified.
Also, do you want to use OUR DTW code? (which is nothing fancy)
Sure, send it over. I probably won’t get a chance to look at it too closely for ~1.5 weeks because I’ll be out of town for for a bit after tomorrow.
Stan
Philip on Feb. 27, 2020, 09:01
For example: Haar wavelets can be computed in O(N) time, but DTW takes O(Nlog(N)) time. However, under almost all circumstances, computing DTW is much faster (partly because most hardware supports it).
IMHO, I wouldn’t consider comparing DTW with hardware support vs. another algorithm without hardware support is fair in terms of algorithmic efficiency. However, it is fine for practitioner purposes.
In our study (as reported in our paper and using our java implementation), fastDTW is faster than fullDTW empirically for “larger” N.
In the caption of your plot (“Fig 1”), it seems you are measuring classification time. Our study does not include the dtw_distance being used for additional/”downstream” tasks such as classification.
Also, it seems you are using warping window size/width/radius on the x-axis and one curve is labeled “iterative cDTW”. What is “cDTW”?
-
if “cDTW” means classic/full DTW, what does “window size/width/radius” mean?
-
If “cDTW” means constraint DTW with a fixed radius, I would not be surprised if it is faster than fastDTW though both are O(N) because:
a. fastDTW would have more overhead in finding the cells to evaluate
b. “radius” in fastDTW is not the same, IMHO, as “radius” in constraint DTW – I would use % of evaluated cells, but I still think fastDTW to be slower because of more overhead in finding the cells.
Eamonn on Feb. 27, 2020, 10:29
IMHO, I wouldn’t consider comparing DTW with hardware support vs. another algorithm without hardware support is fair in terms of algorithmic efficiency. However, it is fine for practitioner purposes.
We 100% agree, and we would never do that (I was just making a point about big oh for small sizes)
In the caption of your plot (“Fig 1”), it seems you are measuring classification time. Our study does not include the dtw_distance being used for additional/”downstream” tasks such as classification.
I cant not see what possible difference this could make.
If I use DTW to do similarity search OR clustering OR classification OR …
It is unstable to measure a single small time on a computer, so we measured 1,000s of small times and summed them. It happens that classification requires computing DTW 1000s of times.
Also, it seems you are using warping window size/width/radius on the x-axis and one curve is labeled “iterative cDTW”. What is “cDTW”?’
cDTW is what most of the community calls DTW with a a warping constraint. Sometime DTW with a warping constraint of say 10% is written as cDTW10
1. if “cDTW” means classic/full DTW, what does “window size/width/radius” mean?
see above
2. If “cDTW” means constraint DTW with a fixed radius, I would not be surprised if it is faster than fastDTW though both are O(N) because:
a. fastDTW would have more overhead in finding the cells to evaluate
b. “radius” in fastDTW is not the same, IMHO, as “radius” in constraint DTW – I would use % of evaluated cells, but I still think fastDTW to be slower because of more overhead in finding the cells.
Yes, that is true.
We are planning to rewrite the paper to correct errors (most of which you pointed out, thanks). And to make our claims narrower and clearer.
thanks
Eamonn
Stan on Feb. 27, 2020, 10:56
I think Dr. Chan made a good observation that I missed in Figure 1. FastDTW only needs to run with a small radius to find the best path through the cost matrix, so comparing DTW and FastDTW at the same radius value does not make sense in a practical sense (although it is a great test to do to measure the DTW vs. FastDTW overhead at the same window radius). It is more accurate to run FastDTW with a small fixed-size radius (not a fixed %, because then it’s not O(N) anymore) and compare that to DTW with a 100% window.
In the java implementation the overhead for fastDTW evaluating the full cost matrix relative to running full DTW (also in Java) was very small in the 10,000 length test so I’m a little skeptical about the FastDTW vs DTW implementations used in Figure 1. I’d expect the FastDTW line in Figure 1 to be just a little bit over DTW due to this test only being on very short time series where FastDTW has ~no expected speedup over DTW (which was not apparent to me until just now)
The Mallat data set used in Figure 1 only contains length 1024 time series and the length of data evaluated in the figure would be more clear if the x-axis was a length rather than a % and if the y-axis was the per-alignment time rather than a total time that naturally implies to the reader that the time series are long in the test. Both of those axes in the current form lead me to believe on first (and 2nd/3rd) reading that much longer time series are being evaluated than is actually the case. It also was not clear to us whether there was a lot of classification-specific “tricks” rather than a straight head-to-head alignment time comparison when looking at that figure. FastDTW is not expected to be faster for such short time series so it’s perhaps not the best test to prove that FastDTW is always slower than DTW (although our expectation was that FastDTW would only be a little bit slower based on our results).
and one more possible example :) …
””” Because of the high frame rate of the features, it is necessary to employ low-cost algorithm. While the original DTW algorithm has O(N^2) time and space complexity, FastDTW operates in O(N) complexity with almost the same accuracy. Müller et al. [13] also examined a similar multi-level DTW for the audio-to-score alignment task and reported similar results compared to the original DTW. “””
Eamonn on Feb. 27, 2020, 11:23
That paper says “Typically, tolerance window with 50 ms is used for evaluation. However, because most of notes were aligned within 50 ms of temporal threshold, we varied the width tolerance window from 0 ms to 200 ms with 10 ms steps”
Lets assume the widest value of 200ms
Lets say you have a two-minute song (about mean length they consider), then the warping window length would be 0.1%. cDTW would be 100 times faster than FastDTW.
They use 100 Hz, so a two minute song is 12,000 datapoints
Renjie. Can you take two random walks of length 12,000
Compare the time for
1) FastDTW with radius 10 [a]
2) cDTW, with w = 0.1% or 12 actual data points
thanks, eamonn
[a] The radius parameter in the fastDTW algorithm, which defines the size of window to find an optimal path for each resolution refinement, was set to 10 in our experiment.
Eamonn on Feb. 27, 2020, 11:33
It also was not clear to us whether there was a lot of classification-specific “tricks” rather than a straight head-to-head alignment time comparison when looking at that figure.
There are ZERO tricks of any kind.
If we used early abandoning LB_Keogh, we would be about 100 times faster on this data (see [a] 4.1.3). But again, we are using zero tricks. This is a head to head comparison.
Thanks for all your great questions and comments, we are rewriting the paper to may our claims clearer.
eamonn
[a] https://www.cs.ucr.edu/~eamonn/SIGKDD_trillion.pdf
Stan on Feb. 27, 2020, 11:58
The radius parameter in the fastDTW algorithm, which defines the size of window to find an optimal path for each resolution refinement, was set to 10 in our experiment.
fyi, in FastDTW the window radius is a radius (goes in each direction), and at full resolution it actually considers this radius on top of the previous resolutions expanded warp wath… so r=10 ~=22 for DTW (10 in each direction plus 2 for the expanded warp path in the middle… the fastDTW radius is also measured diagonally not vertically which can cause some differences depending on how the DTW implementation is doing it.
Philip on Feb. 27, 2020, 13:01
The “downstream” task after algX_DTW matters if algX_DTW is modified to help speed up the combination of algX_DTW and the downstream task. The “downstream” task does not matter if algX_DTW is just a “function call” and is allowed to run completely as if there were no downstream tasks.
Since cDTW is constrained DTW with a fixed radius, it’s O(N) time and space. Though fastDTW is also O(N) time and space, it is slower than cDTW because of more overhead in finding cells. So I doubt we have written in our paper that fastDTW is faster than cDTW theoretically or empirically.
However, for optimal warping paths that are not (or are not known beforehand to be) close to the diagonal, IMHO one of the contributions of fastDTW is the tradeoff between accuracy (with respect to the “correct” distance from fullDTW) and % evaluated cells.
If the optimal warping path is known beforehand to be close to the diagonal, I recommend cDTW and do not recommend fastDTW.
Eamonn on Feb. 27, 2020, 13:05
The “downstream” task after algX_DTW matters if algX_DTW is modified to help speed up the combination of algX_DTW and the downstream task. The “downstream” task does not matter if algX_DTW is just a “function call” and is allowed to run completely as if there were no downstream tasks.
As I said, we are running plain vanilla cDTW, the same algorithm that has been used for over 20 years.
We are making ZERO modifications of any kind.
If the optimal warping path is known beforehand to be close to the diagonal, I recommend cDTW and do not recommend fastDTW.
Duly noted, I will quote you in the paper, and let you edit or remove the quote as you wish, thanks.
Eamonn on Feb. 27, 2020, 18:47
Hi All
I have largely restructured the paper, to be more constructive, to be clearer (although this is only a rough draft), and to take into account your useful comments.
I have added an acknowledgement to you, but I am willing to delete or edit it, if you dont want it.
I will send you a more complete draft in the coming weeks, thanks.
eamonn
Philip on Feb. 28, 2020, 08:41
The following quote may be slightly “out of context”:
‘For this case cDTW is unambiguously faster (see figure X). Moreover, the original authors concede this point, writing in 2020 “If (W) is known beforehand to be (small), I recommend cDTW and do not recommend fastDTW.” [c].’
because Case A seems to have no reference to accuracy with respect to the “correct” distance from fullDTW or knowing the warping path is within the width *beforehand*. FastDTW considers accuracy (as well as speed) and makes weaker assumptions where the warping path could be than cDTW (IHMO).
Also, if we didn’t claim in terms of speed (also in the same email of your quote of my words above), how can we “concede”?
Naturally, the choice of your words is yours.
Therefore, I respectfully request you to remove the quote.
Eamonn on Feb. 28, 2020, 09:32
The following quote may be slightly “out of context”:
‘For this case cDTW is unambiguously faster (see figure X). Moreover, the original authors concede this point, writing in 2020 “If (W) is known beforehand to be (small), I recommend cDTW and do not recommend fastDTW.” [c].’
because Case A seems to have no reference to accuracy with respect to the “correct” distance from fullDTW or knowing the warping path is within the width *beforehand*. FastDTW considers accuracy (as well as speed) and makes weaker assumptions where the warping path could be than cDTW (IHMO).
Also, if we didn’t claim in terms of speed (also in the same email of your quote of my words above), how can we “concede”?
How about…
the original authors echo this point
the original authors agree with this point
the original authors acknowledge this point
As for …“Case A seems to have no reference to accuracy with respect to the “correct” distance from fullDTW”
There is an important point to be made here
cDTWw for w « N, is NOT an approximation to full DTW.
It is its own measure.
Moreover, in the vast majority of cases, it is more accurate for classification or clustering than full DTW.
(99%+ of papers that use DTW use it for classification or clustering )
I know this, because I have tested in on hundreds of datasets, will millions of time series, with billions of pairwise comparisons (https://www.cs.ucr.edu/~eamonn/time_series_data_2018/)
--
Having said that, it seems to be moot, because in Case A, cDTW with w=N, is still is faster than FastDTW with radius = 10.
So even if FastDTW had perfect accuracy relative to full DTW, there would be no reason to use it.
In summary, case A does not need to consider accuracy, it is irrelevant.
cheers
eamonn
Stan on Feb. 28, 2020, 11:40
Eamonn,
I do think there are some serious issues with the experiments behind the cDTW/FastDTW results in Figure1 … apart from it being confusing/misleading to us regarding the length/number of the time series and what “classification” means in those tests. I have some general thoughts on the experiments:
- With our Java implementation of FastDTW and cDTW (looking at the test data that I send to you yesterday), FastDTW is 51% slower than cDTW for an identical “radius” parameter where the same number of “cells” are evaluated at full resolution (the 10K length test with radius=10)… because FastDTW evaluates roughly the same number of cells at lower resolutions also. This very closely matches our theoretical analysis that predicts a 50% overhead at the same radius. The ~cDTW java implementation also has a ~26% overhead in the 10K data point test at radius=10 because it’s a flexible implementation that can take any arbitrary shape window without assuming any constraints (because it is also used in FastDTW to set the window from the lower resolution warp path). This 26% overhead probably decreases down as the radius increases. The results in Figure 1 don’t agree with our theoretical analysis or empirical results. I can’t see how “one or two orders of magnitude faster” is correct without there being some issues with the experiments
- ^This is not saying that FastDTW is always slower. DTW and cDTW must be run with larger “r” values for comparable results with FastDTW. FastDTW is intended to always be run with small “r” values regardless of the length of the time series, and comparing the speed of FastDTW and cDTW where r is a % of a time series does not make sense. Every run of FastDTW is a data point for “Warp Window Size”=100% … the radius parameter is just an accuracy/speed tradeoff that is set to a small value. In Figure 1 FastDTW with small r values is much faster than cDTW at r=100% which is expected. I’m not sure why FastDTW gets so slow for large values of r in Figure 1 (that isn’t what we predict or see empirically) … but that is also a test case that doesn’t happen in normal usage of FastDTW where r is a fixed small value.
- be careful (generally) about how the radius is actually interpreted, FastDTW is interpreting it as a radius and not a width (w~=2r+1)… this may not be an issue, but just making sure
- If the/a Java implementation FastDTW is being called repeatedly from the command line on very small time series, probably 90+% of the time will be spent spinning-up the Java Virtual Machine and then throwing it away and not doing much any work (could be an explanation for results you are seeing)
- if you are confident that the results behind Figure 1 are correct we’d like to see examples of how you ran the tests so we can verify them ourselves
- For comparison of the empirical speed of one algorithm compared to another they should both be implemented in the same language and run in similar conditions … I think you’re already dong this, but it’s worth restating just in case
I have added an acknowledgement to you, but I am willing to delete or edit it, if you dont want it.
I think your acknowledgment is well-worded 🙂
Stan
Eamonn on Feb. 28, 2020, 12:10
With our Java implementation of FastDTW and cDTW (looking at the test data that I send to you yesterday), FastDTW is 51% slower than cDTW for an identical “radius” parameter where the same number of “cells” are evaluated at full resolution (the 10K length test with radius=10)… because FastDTW evaluates roughly the same number of cells at lower resolutions also. This very closely matches our theoretical analysis that predicts a 50% overhead at the same radius. The ~cDTW java implementation also has a ~26% overhead in the 10K data point test at radius=10 because it’s a flexible implementation that can take any arbitrary shape window without assuming any constraints (because it is also used in FastDTW to set the window from the lower resolution warp path). This 26% overhead probably decreases down as the radius increases. The results in Figure 1 don’t agree with our theoretical analysis or empirical results. I can’t see how “one or two orders of magnitude faster” is correct without there being some issues with the experiments
(as I mentioned in an email to Philp)… To be clear “classification” means nothing here.
This figure reflects the time need for 128,975 pairwise comparisons.
The time for just the 128,975 pairwise comparisons, is 99.9999999% of the time reported.
There are no tricks for cDTW (although many many tricks are possible)
The only reason we did 128,975 pairwise comparisons is because doing just one or two would be clearly unstable.
I am not sure what the problem could be here:
1) We are using vanila cDTW, so this is a head to hear comparison.
2) We are using a best faith, fastest implementation of FastDTW. If you have a better implementation, please send it, and we will use it.
3) We are making all the code and datasets publicly available
If you want to design a different experiment that measures the time taken for cDTW vs FastDTW, please carefully describe it, and we will run it.
I will try to write a clarification of r vs w.
^This is not saying that FastDTW is always slower. DTW and cDTW must be run with larger “r” values for comparable results with FastDTW. FastDTW is intended to always be run with small “r” values regardless of the length of the time series, and comparing the speed of FastDTW and cDTW where r is a % of a time series does not make sense. Every run of FastDTW is a data point for “Warp Window Size”=100% … the radius parameter is just an accuracy/speed tradeoff that is set to a small value. In Figure 1 FastDTW with small r values is much faster than cDTW at r=100% which is expected. I’m not sure why FastDTW gets so slow for large values of r in Figure 1 (that isn’t what we predict or see empirically) … but that is also a test case that doesn’t happen in normal usage of FastDTW where r is a fixed small value.
Yes, we are addressing this explicitly in case D, we will send you a preview in a next.
We will also rewite to make your point clear, thanks
be careful (generally) about how the radius is actually interpreted, FastDTW is interpreting it as a radius and not a width (w~=2r+1)… this may not be an issue, but just making sure
cheers
If the/a Java implementation FastDTW is being called repeatedly from the command line on very small time series, probably 90+% of the time will be spent spinning-up the Java Virtual Machine and then throwing it away and not doing much any work (could be an explanation for results you are seeing)
Renjie, lets discuss and test.
Thanks
if you are confident that the results behind Figure 1 are correct we’d like to see examples of how you ran the tests so we can verify them ourselves
As I noted, our plan is
“3) We are making all the code and datasets publicly available”
For comparison of the empirical speed of one algorithm compared to another they should both be implemented in the same language and run in similar conditions … I think you’re already dong this, but it’s worth restating just in case
Yes, we are using the same computer language, same machine, same data (but the data should not matter) etc
thanks
eamonn
Stan on Feb. 28, 2020, 12:38
Eamonn,
To be clear “classification” means nothing here
I understand this after your explained it to me, but if it means nothing I’d suggest not mentioning it to prevent confusion. If what is relevant is that you ran DTW N times, just state that directly.
If you have a better implementation, please send it, and we will use it
This is the one used in the original paper (with some minor bugfixes, the original paper version is 1.0.0)
It probably needs to be run with the flags to run in 64 bit mode and increase the min/max memory to a large amount to avoid using an on disk-swap file
If you want to design a different experiment that measures the time taken for cDTW vs FastDTW, please carefully describe it, and we will run it.
- The most direct comparison is to compare the times of FastDTW with reasonable radius sizes: 5,10,20,40 with cDTW with a 100% warp window (just DTW)
- To determine which is faster in the case where a constrained DTW is wanted/acceptable/preferred … what is faster will depend on FastDTW’s r, cDTW’s r, and the time series length. For this I think it’d be OK to only run FastDTW with a “standard” r=10 for simplicity and evaluate the FastDTW vs cDTW times for different % warp windows and time series lengths. For long time series and large % windows FastDTW will be faster, for short time series and small % windows cDTW will be faster…. with the location of the transition area being the interesting thing to find.
Stan
Eamonn on Feb. 28, 2020, 13:15
Eamonn,
To be clear “classification” means nothing here
I understand this after your explained it to me, but if it means nothing I’d suggest not mentioning it to prevent confusion. If what is relevant is that you ran DTW N times, just state that directly.
Good idea, thanks
If you have a better implementation, please send it, and we will use it
This is the one used in the original paper (with some minor bugfixes, the original paper version is 1.0.0)
It probably needs to be run with the flags to run in 64 bit mode and increase the min/max memory to a large amount to avoid using an on disk-swap file
If you want to design a different experiment that measures the time taken for cDTW vs FastDTW, please carefully describe it, and we will run it.
- The most direct comparison is to compare the times of FastDTW with reasonable radius sizes: 5,10,20,40 with cDTW with a 100% warp window (just DTW)
We are also doing that, in case D
However, as I noted, based on several billion pairwise comparisons, we know that cDTWw for smallish w, is a better distance measure than full DTW.
This fact has been knows since at least 2004 (see fig 6 [a]).
Therefore, the community needs to know how fast cDTW is, over all settings of w.
[a] https://www.cs.ucr.edu/~eamonn/DTW_myths.pdf
- To determine which is faster in the case where a constrained DTW is wanted/acceptable/preferred … what is faster will depend on FastDTW’s r, cDTW’s r, and the time series length.
Yes, this is why we broke it out into four cases. I expect fastDTW will win in case D
For this I think it’d be OK to only run FastDTW with a “standard” r=10 for simplicity and evaluate the FastDTW vs cDTW times for different % warp windows and time series lengths. For long time series and large % windows FastDTW will be faster, for short time series and small % windows cDTW will be faster…. with the location of the transition area being the interesting thing to find.
Yes, we are in the process of finding the location of the transition
thanks
eamonn
We revisit our hypothetical “fall” dataset. We created a data generator that creates two time series of length L seconds. One time series has an immediate fall, then the actor is near motionless for the rest of the time. For the other time series actor is near motionless until just before L seconds are up, then he falls.
It is clear that for cDTW to align the two falls, we must use cDTWN. FastDTW20 should be align them, the original authors not that it is something of a sweet spot “the radius to 20 lowers the error to under 1%” [21]. Note that we do not test to see if FastDTW20 actually aligns the two falls, we simple assume it does. As shown in XXX we can now create pairs of time series of increasing lengths L, and discover at what point FastDTW20 becomes as fast as cDTW.
(to do)
Thus we have found a circumstance where FastDTW20 may become useful. Note that at this breakeven point FastDTW20 an approximation to cDTWN, so cDTWN, is still preferable. However, as L grows each user needs to make decision between time taken vs. utility of approximation. That question is beyond the scope of this paper.
Philip on Feb. 28, 2020, 17:43
I respectfully request you to remove the quote. Thank you for your acknowledgement.
There is an important point to be made here
cDTWw for w « N, is NOT an approximation to full DTW.
It is its own measure.
Moreover, in the vast majority of cases, it is more accurate for classification or clustering than full DTW.
fastDTW is an approximation to full DTW.
We didn’t claim fastDTW is its own measure (we consider full DTW is the “correct” measure).
We didn’t claim fastDTW is more accurate for classification or clustering.
In the context of algX_DTW:
a. is or is not an approximation of full DTW and
b is or is not its own measure (for classification/clustering),
cDTW and fastDTW have different purposes. IMHO comparing two algorithms with different purposes doesn’t seem meaningful to me.
Eamonn on Feb. 28, 2020, 18:05
We didn’t claim fastDTW is its own measure (we consider full DTW is the “correct” measure).
I agree, you did not. We never said otherwise.
However, recall that you do say “FastDTW…compliments existing indexing methods that speed up time series similarity search and classification. “ and “needed to determine similarity between time series and for time series classification” and “ often used to determine time series similarity, classification” etc
In the context of algX_DTW:
Sorry, I do not know what you mean by “algX_DTW “
a. is or is not an approximation of full DTW and
b is or is not its own measure (for classification/clustering),cDTW and fastDTW have different purposes. IMHO comparing two algorithms with different purposes doesn’t seem meaningful to me.
This is not exactly true. cDTW is just the more generalized version of DTW, and FastDTW was introduced as an approximation to DTW.
You could just as easily say “DTW and fastDTW have different purposes. IMHO comparing two algorithms with different purposes doesn’t seem meaningful”, but comparing FastDTW and DTW is exactly what your paper did.
Therefore, the rightmost point of fig 1 is exactly just a comparison of “ full DTW with FastDTW”, which is what your paper did.
We are just ALSO doing a more general case, since almost everyone should be doing constrained DTW (and almost everyone does, see [a])
Thanks.
eamonn
[a] J. Lines and A. Bagnall. Time series classification with ensembles of elastic distance measures. Data Mining and Knowledge Discovery, 29:565–592, 2015.
Philip on Mar. 2, 2020, 09:38
algX_DTW is some algorithm X with DTW in its name.
Let’s first focus on the context in which cDTW and FastDTW are compared (leaving out the comparison between FastDTW with fullDTW for later) in this email. IMHO there are different contexts/purposes. I have been assuming Context/purpose 1 below, but it seems different contexts/purposes are appearing.
Hence, I am not clear in which context cDTW and FastDTW are compared. The 3 contexts below might not include your intended context.
---Context/purpose 1---
Approximating full DTW in terms of distance by a more efficient algorithm (for “larger” N and the “optimal” warping path is not close to the diagonal).
---Context/purpose 2---
Approximation to full DTW in terms of distance is not relevant, the alg is its own measure, getting higher accuracy in a “downstream” task such as classification/clustering is highest in importance, speed is second highest in importance.
---Context/purpose 3---
Approximation to full DTW in terms of distance is not relevant, the alg is its own measure, getting higher accuracy for a “downstream” task such as classification/clustering is not relevant. Only speed is important.
--- FastDTW in the different contexts ---
In Context 1, our study compares FastDTW and cDTW in terms of the tradeoff between accuracy (with respect to the distance from fullDTW) and % of cells evaluated. We consider cDTW and FastDTW are approximations to fullDTW.
In Context 2, since we didn’t claim FastDTW has a higher accuracy than cDTW for a downstream task, IMHO comparing FastDTW and cDTW in speed doesn’t seem meaningful to me.
In Context 3, there are even faster measures than cDTW, which are not approximations to fullDTW and are their own measures; for example, just simply measuring the difference in length between two time series.
Hence, IMHO Context 3 is not meaningful to me.
Eamonn on Mar. 2, 2020 on 10:06
Hi Philip
I responded to the below here and there. But I am a little unsure about some of your claims, so I may not have addressed them fully.
In particular, I am not in some places if you are referring to what your paper said, or what you think now.
---Context/purpose 1---
Approximating full DTW in terms of distance by a more efficient algorithm (for “larger” N and the “optimal” warping path is not close to the diagonal).
We are testing this, and we are going to make N longer and longer, until fastDTW is faster than full DTW. (see ‘fall’ experiment on the next draft)
---Context/purpose 2---
Approximation to full DTW in terms of distance is not relevant, the alg is its own measure, getting higher accuracy in a “downstream” task such as classification/clustering is highest in importance, speed is second highest in importance.
Yes, Case A reflects this. I think about 90% of the published uses of DTW are in this case.
---Context/purpose 3---
Approximation to full DTW in terms of distance is not relevant, the alg is its own measure, getting higher accuracy for a “downstream” task such as classification/clustering is not relevant. Only speed is important.
I dont see this as meaningful or useful (which you seem to state below)
---FastDTW in the different contexts---
In Context 1, our study compares FastDTW and cDTW in terms of the tradeoff between accuracy (with respect to the distance from fullDTW) and % of cells evaluated. We consider cDTW and FastDTW are approximations to fullDTW.
I agree with this.
However, while I agree that you “DTW and FastDTW are approximations to fullDTW.”, I do not see cDTW as being an approximation to Full DTW.
I see it as being a more general measure that includes Euclidean and Full DTW as special cases.
I also advocate exploit the fact that the best w is often very small, both being fast to compute, and allowing lower bounds.
In Context 2, since we didn’t claim FastDTW has a higher accuracy than cDTW for a downstream task, IMHO comparing FastDTW and cDTW in speed doesn’t seem meaningful to me.
That is not quite true. You claim the distance you return in a good approximate of DTW. And downstream algorithms say “given only DTW (or a good approximation of it) this algorithm can do good clustering or classification..” Yo do say “(FastDTW) compliments existing indexing methods that speed up time series similarity search and classification”
In Context 3, there are even faster measures than cDTW, which are not approximations to fullDTW and are their own measures; for example, just simply measuring the difference in length between two time series.
Hence, IMHO Context 3 is not meaningful to me.
I agree 100%, context 3 is meaningless
cheers
Renjie on Mar. 2, 2020, 17:37
If the/a Java implementation FastDTW is being called repeatedly from the command line on very small time series, probably 90+% of the time will be spent spinning-up the Java Virtual Machine and then throwing it away and not doing much any work (could be an explanation for results you are seeing)
Renjie, lets discuss and test.
I forgot to reply this. The measurement is of the function only, not the whole program, so the time spent in setting up Java Virutal Machine is not counted.
In other word, the pseudocode of time measurement is:
startTime = System.currentTimeMillis();
distance = fastDTW(A, B, r); or cDTW(A, B, w);
endTime = System.currentTimeMillis();
elapsed = endTime - startTime;
So the measured time is merely of the algorithm itself (the overhead of function call can be safely ignored, since its contribution is extremely small).
Thanks,
Renjie
Eamonn on Mar. 2, 2020, 17:45
Hi Stan.
We forgot to respond to this point of yours.
We are being very careful not to the time spinning up the JavA VM.
cheers
eamonn
Philip on Mar. 2, 2020, 17:45
Context 2: We didn’t claim FastDTW can get higher accuracy than fullDTW on some downstream task.
downstream algorithms say “given only DTW (or a good approximation of it) this algorithm can do good clustering or classification..”
Looks like they are referring to full DTW and a good approximation, but they didn’t specify which approximation, cDTW could be a good approximation (although you don’t think cDTW is an approximation), there are multiple approximation algorithms. Also, it is in parentheses, so I don’t know if they use a specific approximation algorithm in their experiments.
How many papers use FastDTW to perform classification/clustering and empirically show FastDTW is more accurate than cDTW? I would be interested in seeing the references.
If FastDTW “compliments” other existing indexing methods that would mean FastDTW “praises/admires” the other existing indexing methods. If it was a typo: FastDTW “complements” other existing methods, I would interpret it as FastDTW is an alternative method to improve speed of full DTW (but reducing accuracy in the distance from full DTW), not faster/slower, compared to existing indexing methods.
Eamonn on Mar. 2, 2020, 17:57
Context 2: We didn’t claim FastDTW can get higher accuracy than fullDTW on some downstream task.
Yes, I 100% agree, you do not make that claim.
downstream algorithms say “given only DTW (or a good approximation of it) this algorithm can do good clustering or classification..”
Looks like they are referring to full DTW and a good approximation, but they didn’t specify which approximation, cDTW could be a good approximation (although you don’t think cDTW is an approximation), there are multiple approximation algorithms. Also, it is in parentheses, so I don’t know if they use a specific approximation algorithm in their experiments.
Sorry, to be clear, that sentence “ “given only DTW (or a good approximation of it) this algorithm can do good clustering or classification..” was my shorthand way of summarizing the community of time series researchers. No one literally said this, it is just implicit in thousands of papers.
How many papers use FastDTW to perform classification/clustering and empirically show FastDTW is more accurate than cDTW? I would be interested in seeing the references.
I am aware of zero such papers.
Most papers that us FastDTW do not use cDTW. The only reason they use FastDTW is to avoid using cDTW.
Moreover, your paper never suggests that this is a possibility (that FastDTW is more accurate than cDTW for classification), so I suspect it never occurred to anyone to try. Would you like us to try?
If FastDTW “compliments” other existing indexing methods that would mean FastDTW “praises/admires” the other existing indexing methods. If it was a typo: FastDTW “complements” other existing methods,
What do you mean “if it is a typo”? You wrote this, it is cut and paste from your paper.
I would interpret it as FastDTW is an alternative method to improve speed of full DTW (but reducing accuracy in the distance from full DTW), not faster/slower, compared to existing indexing methods.
Sorry, I just dont understand what you are saying here.
eamonn
Philip on Mar. 3, 2020, 16:36
If “zero papers” provide evidence that FastDTW is more accurate than cDTW in classification/clustering, the relative classification/clustering (downstream) accuracy of FastDTW and cDTW is not known. Hence, only comparing the classification time between FastDTW and cDTW does not seem meaningful to me IMHO (ie, in “Context 3”, not “Context 2”).
You can try to compare the classification accuracy of cDTW, FastDTW and fullDTW. As before, I suggest using % of cells evaluated as the x-axis for cDTW and FastDTW since width in cDTW is different from radius in FastDTW.
“compliments” in your quote is in our paper. Sorry, I meant the typo was ours in our paper, we possibly were thinking “complements”.
Eamonn on Mar. 3, 2020 17:02
If “zero papers” provide evidence that FastDTW is more accurate than cDTW in classification/clustering, the relative classification/clustering (downstream) accuracy of FastDTW and cDTW is not known. Hence, only comparing the classification time between FastDTW and cDTW does not seem meaningful to me IMHO (ie, in “Context 3”, not “Context 2”).
This makes no sense.
You are claiming that FastDTW is a very good approximate to DTW. In the limit, if the approximation is perfect, then then downstream accuracy of clustering and classification will be identical. You do even experiments showing that as you increase r, you tend towards a perfect approximation.
At best, the downstream accuracy of clustering and classification of FastDTW is the same as FullDTW or cDTW (your correctly never claim otherwise).
So let us make the BEST assumption for FastDTW, for a reasonable radius, it is as good as FullDTW or cDTW.
Then the only question is, it is faster? We will test that.
You can try to compare the classification accuracy of cDTW, FastDTW and fullDTW. As before, I suggest using % of cells evaluated as the x-axis for cDTW and FastDTW since width in cDTW is different from radius in FastDTW.
I have done this a over decade ago.
1) In general cDTW is much more accurate than FullDTW. Those results are public here https://www.cs.ucr.edu/~eamonn/time_series_data_2018/
2) cDTW is much more accurate than FastDTW (unsurprising, given ‘1’ and the fact that FastDTW approximates Full DTW)
3) If you add the same constraint to FastDTW as cDTW, then the gap closes greatly, and FastDTW is almost as accurate as cDTW.
eamonn
Eamonn on Mar. 4, 2020, 10:31
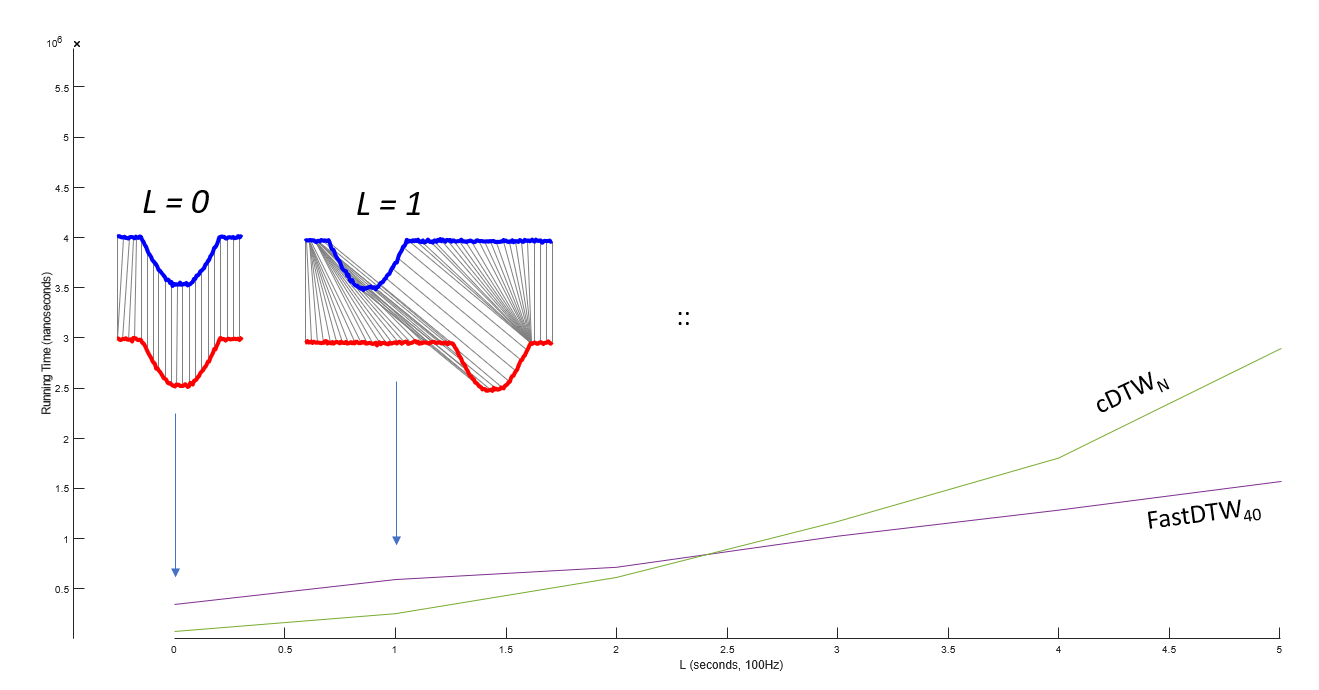
This is a first look, we need to clean up the figures. When the length of the time series is 3 seconds or greater, with no warping constraint on DTW, then FastDTW is faster
Stan on Mar. 4, 2020, 13:51
Eamonn,
The data backing this figure looks good to me. Reasonable implementation will disagree by reasonable amounts… and this is reasonable :)
Stan
Eamonn on Mar. 4, 2020, 13:56
Thanks.
We are working hard to temper our claims, and write the most positive paper possible.
We have already changes the title etc.
We will give you the paper in a week or so, and let you suggest edits or experiments.
Best wishes
Philip on Mar. 4, 2020, 17:56
If previously you have shown that cDTW is more accurate than FastDTW in classification, comparing classification time would be meaningful.
May I have the reference to the publication? A quick search on “fastdtw cdtw keogh” at Google Scholar doesn’t seem to find it.
Eamonn on Mar. 4, 2020 17:35
If previously you have shown that cDTW is more accurate than FastDTW in classification, comparing classification time would be meaningful.
Sorry, that does not follow. I do not understand any reason why anyone would care. It would add nothing, and distract from our paper.
If you want to design an experiment, and the metrics to measure. I will do it, and put in on the papers website as a favor to you. But it would tell the world nothing.
May I have the reference to the publication? A quick search on “fastdtw cdtw keogh” at Google Scholar doesn’t seem to find it.
I compared the accuracy of fullDTW with cDTW, SWALE, SPADE, EPR, LCSS, TQuest, and FastDTW and a dozen or so others.
But when I wrote the paper, I only kept in fullDTW with cDTW, SWALE, SPADE, EPR, LCSS, TQuest
Here is the paper https://www.cs.ucr.edu/~eamonn/vldb_08_Experimental_comparison_time_series.pdf
I could not include everything. Besides, as I noted above “ FastDTW is a good approximation to FullDTW “ so it was redundant.
eamonn
Philip on Mar. 5, 2020, 16:45
Whether you run experiments is your decision.
Here are some speculations/thoughts:
-
FastDTW is an approximation to fullDTW, but the smaller the radius is, the poorer the approximation. I consider cDTW is also an approximation to fullDTW (although you don’t think that way). cDTW with a smaller width is a poorer approximation to fullDTW, but ignoring less important information becomes more accurate than fullDTW in classification. Possibly, FastDTW with a small radius (but not too small) might ignore less important information and benefit classification.
-
Characteristics of the data probably play an important role. cDTW with a small width is more accurate than fullDTW when the optimal warp path is close to the diagonal (in a majority of your datasets). If the optimal (or “needed”) warp path is not close to the diagonal, cDTW with a small width might not be more accurate than fullDTW in classification. (FastDTW is also designed for this case as discussed before.)
Eamonn on Mar. 5, 2020 17:01
We have explicitly tested ‘2’ below. What you say is true, and it will be in the paper.
---
For ‘1’. You would be surprised at how often the best warping path is close to the diagonal.
An independent group measured this fact (and exploited this fact). See figure 5 of [a].
However, I dont see that it is relevant.
If you want high classification accuracy, learn the best value of w for your dataset. As the histogram below shows, 97% of the time, it is less than 20%, 80% of the time it is less than 10%
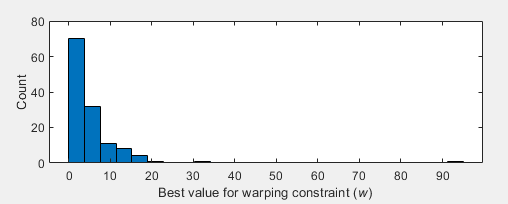
cDTW is generally a MUCH better distance measure than Full DTW, independent of speed. eamonn
[a] Chang Wei Tan, Matthieu Herrmann, Germain Forestier, Geoffrey I. Webb, François Petitjean: Efficient search of the best warping window for Dynamic Time Warping. SDM 2018: 225-233
Eamonn on Mar. 7, 2020, 17:03
Hello
The paper is still rough, however I am 99% certain that we have done every experiment we plan to do (here, less is more!)
We plan to clean it up next week, publish on https://arxiv.org/, and submit to TKDE.
Again thanks for your feedback. I understand FastDTW much better than I did 3 weeks ago.
Eamonn